< Previous

Les études des facteurs potentiellement associés à la survie sont quasiment toutes basées sur l’estimateur de Kaplan-Meier et/ou sur le modèle de Cox. Ces méthodes permettent l’étude du temps d’apparition d’un événement unique. Trois choix de variables à expliquer sont possibles pour les études de survie en transplantation rénale : (i) le délai entre la greffe et le retour en dialyse (les décès avec un greffon fonctionnel sont alors des censures à droite), (ii) le délai entre la greffe et le décès avec un greffon fonctionnel (les retours en dialyses sont alors des censures à droite) et (iii) le délai entre la greffe et le premier des deux échecs possibles. La première solution est critiquable puisqu’un nombre non-négligeable de décès est dû à la greffe ou à sa prise en charge. L’équipe a d’ailleurs montré l’augmentation du risque de cancers dus aux traitements immunosuppresseurs. La surestimation de la survie qui en découle n’est pas le seul problème de cette approche. En effet, le modèle de Cox suppose une indépendance entre le processus de censure et le temps de survie étudié. Cette hypothèse est difficilement acceptable puisque le niveau de filtration glomérulaire est lié à de nombreuses comorbidités. Le deux autres choix sont à l’inverse les plus pessimistes. Ils considèrent tous les décès comme liés à la transplantation alors que beaucoup d’entre eux sont indépendants de la pathologie étudiée. De plus, il est admis que cette stratégie est synonyme de pertes d’informations puisqu’un effet moyen des facteurs de risque est modélisé, alors qu’une même variable peut avoir des effets différents selon l’échec (décès ou retour en dialyse). Aujourd’hui, le consensus est de présenter les deux modèles dans les résultats des analyses de survie. L‘idée admise est qu’une certaine vérité est intermédiaire entre les deux modèles, hypothèse acceptable si l’on considère que le modèle de Cox est le seul possible.

En transplantation rénale, Gjertson et al. ont été les premiers à utiliser une approche plus générale permettant l’analyse d’événements en compétition. Nous avons depuis montré que des développements méthodologiques dans cette voix permettaient d’améliorer les connaissances issues d’analyse de survie. Nous avons utilisé des modèles multi-états qui généralisent les modèles à risques compétitifs (figure 1). Nous avons en particulier adapté l’approche semi-Markovienne à l’évolution des patients transplantés en prenant en compte la censure par intervalle des temps de transitions (l’état de santé d’un patient n’est pas forcément connu entre deux visites) et en proposant un test d’adéquation des temps d’attente avant les transitions. Ces développements ont été réalisés pendant la thèse de Biostatistique de Y. Foucher (manuscrit, présentation orale).

Application à la cohorte DIVAT

Si on compare les résultats obtenus avec de tels modèles par rapport au modèle de Cox (à partir des mêmes données), il est évident au regard des figures 1 et 2 que les conclusions qui découlent du modèle semi-Markovien sont beaucoup plus riches, particulièrement en terme d’évaluation des facteurs déterminants l’évolution.

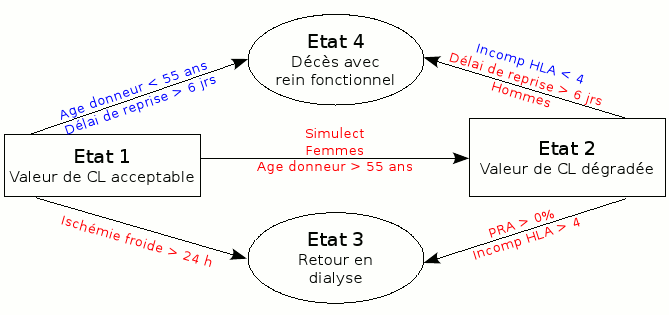
Figure 1 : Résultats obtenus à partir d’un modèle semi-Markovien estimé chez les mêmes patients (n=900, DIVAT Nantes).

Figure 2 : Résultats obtenus à partir d’un modèle de Cox estimé chez les mêmes patients (n=900, DIVAT Nantes).

A partir du modèle semi-Markovien, on retrouve de manière significative la corrélation entre une partie de l’évolution du patient et l’âge du donneur, le délai de reprise au démarrage de la fonction rénale, le nombre d’incompatibilités HLA, le sexe du receveur, la nature du traitement immunosuppresseur, le temps d’ischémie froide et l’immunisation (PRA). Parallèlement, si on analyse la survie du patient et du greffon de manière plus classique, il existe clairement une perte d’information. En effet, seul le délai de reprise de la fonction rénale et les âges du donneur et du receveur sont alors identifiés comme des déterminants importants. Cette différence entre les deux approches peut être expliquée en grande partie par le fait que la stratégie multi-états correspond mieux à la réalité clinique de l’évolution du patient en proposant une évolution progressive et en distinguant le décès et le retour en dialyse comme deux échecs non-comparables. C’est cette caractéristique que nous voulons approfondir en potentialisant les capacités pronostiques des variables grâce à leur association spécifique à certaines étapes du processus d’évolution.

Publications

Pour plus de détails, en particulier sur les aspects statistiques permettant l’obtention de tels résultats, vous trouverez les travaux scientifiques de notre équipe à partir des liens suivants :

Articles originaux :

Foucher Y, Giral M, Soulillou JP, Daures JP. "Time-dependent ROC analysis for a three-class prognostic with application to kidney transplantation." Statistics in medicine 2010, in press.
Foucher Y, Giral M, Soulillou JP, Daurès JP."A flexible semi-Markov model for interval-censored data and goodness-of-fit testing."Statistical Methods in Medical Research 2010 Apr;19(2):127-145. (Pubmed Link)
Foucher Y, Giral M, Soulillou JP, Daures JP."A semi-Markov model for multistate and interval-censored data with multiple terminal events. Application in renal transplantation."Statistics in medicine 2007 Dec 30; 26(30):5381-5393. (Pubmed Link)

Communications orales :

Foucher Y, Rigouin P, Akl A, Launay K, Landais P, Duny Y, Daures JP, Giral M. "The modeling of the evolution of kidney transplant recipients : Applications to the DIVAT cohort." International Society for Clinical Biostatistics (Montpellier, France). 2010.
Foucher Y, Giral M, Soulillou JP, Daurès JP. "Time-dependent ROC analysis for a three-class prognostic." International Society for Clinical Biostatistics (Prague, République Tchèque). 2009.
Giral M, Foucher Y, Daurès JP, Soulillou JP. ""New tool to analyse confounding factors in kidney graft outcome: A DIVAT data base study."" American Transplant Congress (Toronto, Canada). 2008.
Foucher Y, Giral M, Soulillou JP, Daurès JP. "Modèle semi-Markovien avec double censure par intervalle et test d’adéquation." Congrès de la Société Française de Statistiques (Angers, France). 2007.
Foucher Y, Giral M, Soulillou JP, Daurès JP. ""A semi-Markov model for interval-censored data and multiple events: Application to the evolution of kidney transplant recipients."" (Genève, Suisse). 2006.
Foucher Y, Giral M, Soulillou JP, Daurès JP. ""A semi-Markov Model with Interval Censoring and Non-Proportional Hazards."" International Biometric Conference (Montréal, Canada). 2006.